身为一个通常都不会迟到的好人,常常会奇怪,为什么无论是上学还是上班的时候,总是住家比较远(比如在下)的人反而到的很早,步行几分钟就可以赶到的人却往往是刚好踩点呢?
为此,我想用统计分析的方法找到其中的原因。
首先第一步的工作,就是:
伪!造!数!据! 囧 :023:
2个对象合计1200次的实地统计要1年多才可以完成啊,为了证明我一点也不宅,所以可耻地用伪造的正态分布曲线代替了。这样读者也可以看得轻松一点不是吗?(读者:喂!我们是要看没有操守的你被教授持刀追杀啦!)
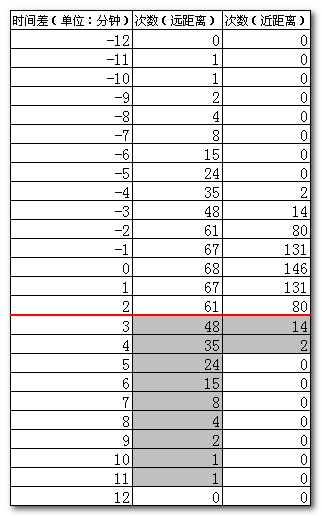
以下就是伪造的到达时间统计表,其中时间差表示到达时间和准点时间的差值,右侧两列则分别是住处离目的地距离较远和距离较近的到达次数统计值。
假设条件是,路上的耽搁使得到达时间分布扩散,但仍基本符合正态分布规律。距离越远的,分布扩散越明显。
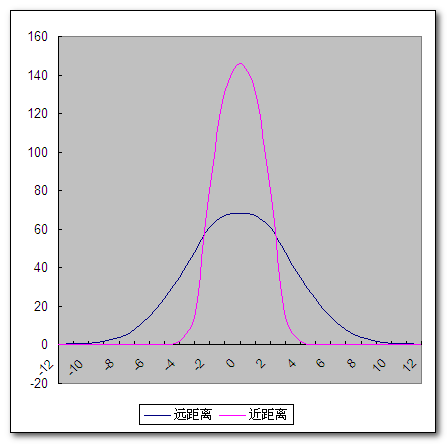
然后是相对应的曲线图。
现在假设迟到的时间点设置在+3之前(如红线所示),则距离较近者会有14+2=16次迟到(灰色部分),而不幸的距离较远者会有48+35+24+15+8+4+2+1+1=138次迟到。23%的迟到率,这显然也会被教授或老板拿着刀追砍。
距离较远者要达到16次以下的迟到次数,迟到时间点应定在+7之前才较为合适,即推迟4分钟。而现在,他必须为这缩减的4分钟付出代价,也就是比先前整体早到4分钟,才能达到+3时间点的要求。
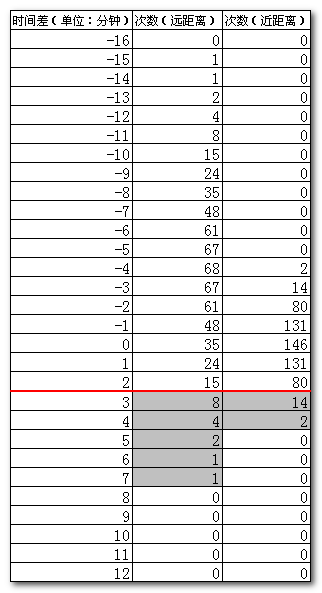
于是经过调整之后的到达时间统计表就成了如下所示,两个人的迟到次数终于扯平了:
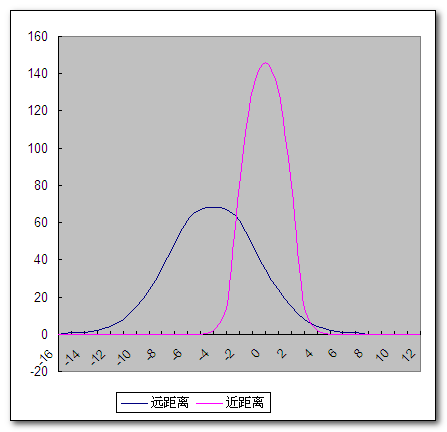
相应的曲线图变成了这样,距离较远者的统计曲线左移了4个横轴单位:
从第2个曲线图中可以明显的看到,距离较远者不但早到的次数远远超出,而且提早时间的最大值也从之前的7分钟变为了11分钟——即平移的时间,如果你有兴趣,还可以算一算距离较近者发现对方比自己到得早的概率有何变化。
综上所述,假如距离越远,在路上耽搁时间的事件发生几率越高,则距离较远者必须比原始的方案越提早到达,才能保证迟到的可能性与距离较近者差不多。当然,这一结论完全是建立在一厢情愿的假设和无耻的伪造数据上的,是不是符合事实,就要等人实际验证了。何况有的人对迟到和被追杀完全不在意,又或者在遭遇麻烦时有超强的时间掌控能力。